黄河交通学院2024年单独招生《文化素质测试》考试大纲

一、考试性质

黄河交通学院单独招生普通类《语文数学英语》考试是由合格的高中毕业生和具有同等学力（中职、社会考生，下同）的考生参加的选拔性考试。学校按已确定的招生计划，根据考生成绩，择优录取。根据普通高等学校对学生文化素质的要求，依据中华人民共和国教育部颁布的《普通高中课程方案（实验）》、《普通高中语文课程标准（实验）》、《普通高中数学课程标准（实验）》和《普通高中英语课程标准（实验）》，确定本考试要求及考试内容，对考生的文化素质知识水平进行书面考核。

二、考试形式与试卷结构

（一）考试形式

笔试

（二）考试时长与分值

1.考试时长为100分钟。

2.试卷总分200分，其中语文100分、数学60分、英语40分。

（三）试题类型及分值构成

1.语文：判断题（10分）、选择题（20分）、填空题（10分）、阅读理解（20分）、作文（40分）

2.数学：选择题（30分）、填空题（16分）、解答题（14分）

3.英语：情景交际（10分）、选择题（20分）、阅读理解（10分）

三、考试内容及要求

（一）语文部分

1.语言基础知识和语言表达

（1）汉字

识记现代汉语普通话的常见字的字音、常见汉字的字形。

（2）词语

正确使用常见词语（包括实词、虚词、成语）。

（3）句子

①辨析病句

病句类型：成分残缺或赘余、搭配不当、语序不当、表意不明、不合逻辑、关联不当。

②变换句式

包括：主动句与被动句（包括“把”字句）、肯定句与否定句，以及陈述句、祈使句、疑问句和感叹句之间的变换。

③正确使用标点符号

④鉴别常见修辞手法（比喻、拟人、借代、夸张、对偶、排比、设问、反问等）。

包括：不同的比喻、借代、夸张、比拟、设问、反问、排比、对偶。

2.文学常识

识记课文内中国重要作家及其时代和代表作，识记课文内外国重要作家、国别及代表作；了解诗歌、散文、小说、戏剧的基本特点，了解课文文学作品中人物、情节、环境特点及作品的主要艺术手法。

3.现代文阅读

（1）理解文中重要词语和句子的含义，把握和筛选文中的信息。

（2）把握文章的基本观点或文章主旨。

（3）理解作品中人物以及作者的思想情感。

（4）掌握文章的文体特点：理清说明文的说明顺序与方法；把握议论文三要素的逻辑关系及论证方法；能分析叙事文学作品中人物描写的手段—肖像、神态、动作、语言、心理，情节的安排—顺叙、倒叙、插叙以及自然环境、社会环境的描写对刻画人物、加深主题、渲染气氛所起的作用；能找出结构散文的主要线索。

4.古代诗文阅读欣赏

理解常见文言实词在文中的含义，尤其能辨析一词多义在不同语境中的不同含义及古今词义的区别；理解常见文言虚词在文中的意义和用法（之、其、而、以、为、安、耳、夫、焉、乎、也）；理解与现代汉语不同的文言句式和用法（判断句、被动句、省略句、倒装句、状语后置、宾语前置、定语后置、词类活用等）；理解并翻译浅易的文言句子；筛选文中信息，概括中心意思，评价作者观点；鉴赏浅易的古典诗词，包括词义解释、作品思想内容和情感的把握，表达技巧和诗歌风格的鉴赏等。

5.作文

命题形式包括命题作文、话题作文、半命题作文、材料作文、选题作文等。

要求：符合题意、中心明确、思想健康；选材得当、结构完整、语句通顺；有真情实意，写出自己对自然、社会和人生的热爱和体验或对职业生涯的思考和规划；书写规范，不写错别字，正确使用标点符号。

写记叙文，能恰当地选择材料和组织材料，能在叙述和描写的基础上合理运用抒情、议论等多种表达方式；写说明文，能把握说明对象的特征，合理安排说明顺序，恰当运用常见的说明方法；写应用文，做到格式规范，文字简约，能够根据学习、生活、职业工作的需要恰当运用。

（二）数学部分

    考试内容包含集合与常用逻辑用语、函数、方程与不等式、数列、平面向量、排列组合与二项式定理、三角函数、解析几何、立体几何、概率与统计初步十个部分。具体内容和要求如下：
    1.集合与常用逻辑用语
   （1）集合
    集合的概念，集合的表示法，集合之间的关系，集合的基本运算。
    要求：
   ①理解集合的概念，掌握集合的表示法，掌握集合之间的关系（子集、真子集、相等)，掌握集合的交、并、补运算。
   ②理解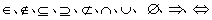等符号的含义，并能用这些符号表示集合与集合、元素与集合、命题与命题之间的关系。

（2）常用逻辑用语

命题、量词、逻辑联结词。

要求：
①了解命题的有关概念。
②了解量词的有关概念，理解全称量词和存在量词的意义，会用相应的符号表示。
③理解逻辑联结词“且”、“或”、“非”的意义。

2.函数

函数的概念，函数的表示方法，函数的单调性、奇偶性。分段函数，一次函数、二次函数的图象和性质、指数（零指数、负整指数、分数指数）的概念，实数指数幂的运算法则。指数函数的概念，指数函数的图象和性质。对数的概念，对数的性质与运算法则。对数函数的概念，对数函数的图象和性质。

要求：

（1)理解函数的概念及其表示法，会求一些常见函数的定义域。
    （2）理解函数符号f(x)的含义，会由f(x)的表达式求出f(ax+b)的表达式。

（3）理解函数的单调性、奇偶性，掌握增函数、减函数、奇函数、偶函数的图象。
    （4）理解分段函数的概念。
    （5）理解二次函数的概念，掌握二次函数的图象和性质。
    （6）会求二次函数的解析式，会求二次函数的最值。
    （7）能灵活运用二次函数的知识解决简单的有关问题。
    （8）理解有理指数的概念，会进行有理指数幂的计算。
    （9）了解对数的概念，理解对数的性质和运算法则。

（10）理解指数函数、对数函数的概念，掌握其图象和性质。

（11）能运用指数函数、对数函数的知识解决简单的有关问题。
    3.方程与不等式
    配方法，一元二次方程的解法，实数的大小，不等式的性质，区间，含有绝对值的不等式的解法，一元二次不等式的解法。
    要求：
     (1）学握配方法，会用配方法解决有关问题。
    （2）会解一元二次方程。

（3）学握不等式的性质。

（4）会解一元一次不等式（组），会用区间表示不等式的解集。

（5）会解形如|ax+b|≥c或|ax+b|＜c的含有绝对值的不等式。

（6）会解一元二次不等式。

（7）能利用不等式的知识解决简单实际问题。

 4.数列

数列的概念。等差数列及其通项公式，等差中项，等差数列前n项和公式。等比数列及其通项公式，等比中项，等比数列前n项和公式。
    要求：
   （1) 理解数列概念和数列通项公式的意义。
   （2）掌握等差数列和等差中项的概念，掌握等差数列的通项公式及前n项和公式，并能解决简单的实际问题。

（3）掌握等比数列和等比中项的概念，掌握等比数列的通项公式及前n项和公式，并能解決简单的实际问题。
    5.平面向量
    向量的概念，向量的线性运算，向量坐标的概念，向量的坐标运算，中点公式。向量夹角的定义，数量积，两向量垂直、平行的条件。

要求：

（1）理解向量的概念，会正确进行向量的线性运算（加法、减法和数乘向量、数量积）。
    （2）掌握向量的坐标与点坐标之间的关系，掌握向量的坐标运算。
    （3）掌握两向量垂直、平行的条件。
    （4）学握中点公式、距离公式。
    （5）掌握向量夹角的定义，向量内积的定义、性质及其运算。掌握向量内积的直角坐标运算。

6.排列、组合与二项式定理

分类计数原理与分步计数原理。排列的概念，排列数公式。组合的概念，组合数公式及性质。二项式定理、二项式系数的性质。

要求：

（1）理解分类计数原理及分步计数原理，会用这两个原理解决一些较简单的问题。

（2）理解排列和排列数的意义，会用排列数公式计算简单的排列问题。

（3）理解组合和组合数的意义及组合数的性质，会用组合数公式计算简单的组合问题。

（4）掌握二项式定理，理解二项式系数的性质。

7.三角函数

角的概念的推广、弧度制。任意角三魚函数（正弦、余孩和正切）的概念，同角三角函数的基本关系式。三角函数诱导公式。三角函数（正弦和余弦）的图象和性质。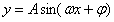的图象和性质。己知三角函数值求指定范围内的角。和角公式，倍角公式。正弦定理、余弦定理及三角形的面积公式。
    要求：
  （1）了解终边相同的角的集合。
  （2）理解弧度的意义，掌握弧度和角度的互化．
  （3）理解任意角三角函数的定义，掌握三角函数在各象限的符号和同角三角函数间的基本关系式。
  （4）会用诱导公式化简三角函数式。
  （5）掌握正弦函数、正弦型函数的图像和性质（定义域、值域、周期性、奇偶性、单调性）。了解余弦函数的图象和性质。
  （6）会用三角函数（正孩和余孩）值求出指定范围内的角。
  （7）掌握和角公式与倍角公式，会用它们进行计算、化简和证明。
  （8）会求函数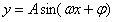的最值。
  （9）掌握正弦定理和余弦定理。会根据已知条件求三角形的边、角及面积。
   8.解析几何
   直线的方向向量与法向量的概念，直线倾斜角、斜率的概念，直线方程的点斜式及斜截式、一般式。两条直线垂直与平行的条件，点到直线的距离。圆的标准方程和一般方程。待定系数法。椭圆的标准方程和性质。双曲线的标准方程和性质。抛物线的标准方程和性质。
   要求：
  （1）了解直线的倾斜角和斜率的概念，掌握直线的点斜式方程及一般式方程。
  （2）会求两曲线的交点坐标。
  （3）会求点到直线的距离，掌握两条直线平行与垂直的条件。
  （4）掌握圆的标准方程和一般方程以及直线与圆的位置关系，能灵活运用它们解决有关问题。

（5）了解待定系数法的概念，会用待定系数法解决有关问题。

（6）掌握圆锥曲线（椭圆、双曲线、抛物线）的概念、标准方程和性质，能灵活运用它们解决有关问题。

9.立体几何

多面体、旋转体和棱柱、棱锥、圆柱、圆锥、球的概念。柱体、锥体、球的表面积和体积公式。平面的表示法，平面的基本性质。空间直线与直线，直线与平面，平面与平面的位置关系。直线与平面、平面与平面的两种位置(平行、垂直）关系的判定与性质。点到平面的距离、直线到平面的距离、平行平面间的距离的概念。
    要求：
   （1）了解多面体、旋转体和棱柱、棱锥、圆柱、圆锥、球的概念。
   （2）掌握柱体、锥体、球的表面积和体积公式。
   （3）了解平面的基本性质。
   （4）理解空间直线与直线，直线与平面，平面与平面的位置关系。
   （5）理解直线与直线、直线与平面、平面与平面的两种位置(平行、垂直）关系的判定与性质。
   （6）了解点到平面的距离、直线到平面的距离、平行平面间的距离的概念，并会解决相关的距离问题。
    10.概率与统计初步
    样本空间、随机事件、基本事件、古典概型、概率的简单性质。直方图与频率分布，总体与样本，抽样方法（简单的随机抽样，系统抽样，分层抽样)。

要求：

（1）了解样本空间、随机事件、基本事件、古典概型等概念及概率的简单性质，会利用古典概型解决一些简单的实际问题。
    （2）了解直方图与频率分布，理解总体与样本，了解抽样方法。
    （3）能运用概率、统计初步知识解决简单的实际问题。

（三）英语部分

1.语言知识

（1）能够掌握2200个英语单词和400个习惯用语或固定搭配。

（2）能够掌握并能运用英语语音基础知识，掌握英语单词的基本拼读规则以及句子重音、英语语调等内容。

（3）能够理解并正确使用以下基本英语语法知识：

名词：可数名词及其单复数、不可数名词、专用名词、名词所有格

代词：人称代词、物主代词、反身代词、指示代词、不定代词、疑问代词

数词：基数词、序数词

介词和介词短语

连词：并列连词、从属连词

形容词（比较级和最高级）

副词（比较级和最高级）

冠词：不定冠词、定冠词、零冠词

动词：动词的基本形式、系动词、及物动词和不及物动词、助动词、情态动词

时态：一般现在时、一般过去时、一般将来时、现在进行时、过去进行时、过去将来时、将来进行时、现在完成时、过去完成时、现在完成进行时

被动语态

非谓语动词：动词不定式、动词的-ing形式、动词的-ed形式

构词法：合成法、派生法、转化法、缩写和简写

句子种类：陈述句、疑问句、祈使句、感叹句

句子成分：主语、谓语、表语、宾语、定语、状语、补语

简单句的基本句型

主谓一致、并列复合句、间接引语、省略、倒装、强调、虚拟语气

主从复合句：宾语从句、状语从句、定语从句、主语从句、表语从句

（4）能够掌握以下日常生活及通用职业场景下的基本交际用语

问候与道别（Greeting and saying goodbye）

引荐与介绍（Introducing oneself and others）

感谢与道歉（Expressing thanks and making apologies）

预约与邀请（Making appointments and invitations）

祝愿与祝贺（Expressing wishes and congratulations）

求助与提供帮助（Asking for and offering help）

赞同与反对（Expressing agreement and disagreement）

接受与拒绝（Accepting and rejecting）

询问与提供信息（Seeking and offering information）

劝告与建议（Giving advice and making suggestions）

2.语言运用

（1）情景交际：以情景为条件，以对话为主要表达形式；既短小又灵活，前言后语连接紧凑，答语多呈现省略，增加了答案的隐蔽性；主要考察英语的日常用语、习惯用语以及各种场合的交际性语言，并从实际出发，考查交际语言的运用能力。

要求：具有在具体的语言环境中实际运用所学语言知识交流思想、表达观点的能力。

（2）单项选择：了解单项选择的命题特点，考查考生对语法和习语的识记、理解和运用能力。要求考生能够在特定的环境中正确辨别单词和词汇及灵活运用语法和固定搭配。

要求：要有牢固的语言基础知识，能够在特定的语言环境中正确、熟练地运用所学的语法、词汇知识；具有快速阅读和整体理解语句的能力，能够根据上下文线索通篇考虑的能力；结合个人所具有的各方面的知识（包括话题等方面的知识）、逻辑推理能力以及语言使用的相关经验做出正确的判断和最佳选择的能力。

（3）阅读理解：了解阅读理解题的命题特点，掌握此题型的基本解题思路与解题步骤。能读懂书、报、杂志中关于一般性话题的简短文段以及公告、说明、广告等，并能从中获取相关信息。

要求：理解主旨要义；理解文中具体信息；根据上下文推断单词和短语的含义；理解段落中各句子之间的关系，做出判断和推理；理解文章的基本结构；理解作者的意图、观点和态度。